
四元數是什麼 將你想要的旋轉轉換成四元數 怎麼使用四元數對一個點/向量進行旋轉
這篇文章是一篇國外文章的粗略翻譯加上一些不專業註解,希望大家在等待泡麵的同時可以快速學會使用這個工具,克服這個多數人心中的數學惡夢
一句話解釋四元數
一個四元數可以被視為繞任意軸的旋轉
原文
A quaternion can be seen as a object that holds a rotation around any axis
影片互動示意解說
那為什麼這個工具這麼神,讓你願意犧牲等泡麵追劇的時間來學習呢? 因為平常如果我們不使用四元數,還要進行物體的旋轉,我們會需要使用矩陣來進行旋轉(以下附上公式),而使用矩陣你除了需要記憶下面這些sin跟cos的位置以外,你還需要關心你使用矩陣的順序,也就是說你先對x軸在對y軸的旋轉不一定會等於先進行y軸在對x軸的旋轉,使用起來其實有一定程度的不方便,再加上各個3D引擎使用的旋轉順序不盡相同
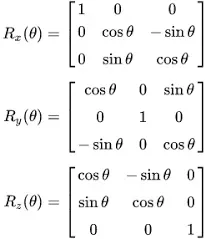
這時候拯救你睡眠時間跟追劇時間的救星出現了,不要看四元數外表醜陋,其實他內心很可愛,好東西怎麼可以不拿來用呢?
以下開始介紹我們今天的主角"四元數"
四元數是由實數與虛數兩個部分組成的複數(complex numbers) s 代表實數部分 v代表虛數部分
q = [s,v]
q = [s + xi + yj + zk]
在3D軟體編程中我們通常使用以下格式,而其中的 w=s 而 [x,y,z]=v
q = [x, y, z, w]
其實也很簡單你只需要下面這個公式就可以了
p1 = q P0 q^-1
p1 : 旋轉過的點/向量 p0 : 選轉前的點/向量 q : 四元數 q^-1 : 四元數的倒數
等等先不要走,我知道這個還不夠簡單,光是要能夠執行上面的公式你還需要知道四件事:
怎麼將繞任意軸旋轉變成四元數 怎麼將點/向量變成四元數 怎麼取得四元數的倒數 怎麼對兩個四元數相乘 p.s-1 以下出現的四元數都是預設使用單位四元數,也就是正規化(大小為一)的四元數
p.s-2 以下解說過程只關心實現過程,不關心原理以及證明過程
在這個步驟你需要兩個資訊
選轉軸是誰 選轉幾度
//known info : angle and axis
half_angle = angle/2
q.x = axis.x * sin(half_angle)
q.y = axis.y * sin(half_angle)
q.z = axis.z * sin(half_angle)
q.w = cos(half_angle);
q.x = position.x
q.y = position.y
q.z = position.z
q.w = 0
q = [x, y, z, w]
norm = |q| = sqrt(q.x^2 + q.y^2 + q.z^2 + q.w^2)
q^-1 = [-x, -y, -z, w]/ norm
q^-1 = [-x/norm, -y/norm, -z/norm, w/norm]
but !!如果我們的四元數是單位四元數那就可以直接變成
q^-1 = q* = [-x, -y, -z, w]
首先 四元數是可以相乘的
q = q1 * q2
但 四元數並不滿足交換率也就是說
q1 * q2 != q2 * q1
他們乘起來的結果就是 :
q.x = (q1.w * q2.x) + (q1.x * q2.w) + (q1.y * q2.z) - (q1.z * q2.y)
q.y = (q1.w * q2.y) - (q1.x * q2.z) + (q1.y * q2.w) + (q1.z * q2.x)
q.z = (q1.w * q2.z) + (q1.x * q2.y) - (q1.y * q2.x) + (q1.z * q2.w)
q.w = (q1.w * q2.w) - (q1.x * q2.x) - (q1.y * q2.y) - (q1.z * q2.z)
其實你並不需要真的把上面的結果記起來,大部分的使用情境下都有現成的函式庫或者模組可以幫你做完運算,你只需要知道你這次旋轉要圍繞哪個軸,並且旋轉多少度,在按照上面的步驟依序運算就可以得到你要的答案了
p.s. 會長這麼醜是因為四元數的定義
i^2 = j^2 = k^2 = -1
ij = -ji = k
jk = -kj = i
ki = -ik = j
放上一張紀念圖

現在~泡麵應該好了,趕快回去吃吧~
